全部分类/
教育教学/
高中数理化

高中数理化

2025年23期

北师大集团核心刊物

扫码免费借阅

目录

快速导航

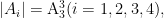
名师工作室 | 关键能力的培育路径探究

名师工作室 | 关键能力的培育路径探究

2020年教育部考试中心发布了《中国高考评价体系》，为中国的新高考改革吹响了冲锋的号角.《中国高考评价体系》的一大亮点就是强调培养学生的关键能力，其指出“关键能力是指即将进入高等学校的学习者在面对与学科相关的生活实践或学习探索问题情境时，高质量地认识问题、分析问题、解决问题所必须具备的能力."具体来讲，关键能力是指学生对信息识别与加工、逻辑推理与论证、科学探究与思维建模、语言组织与表达、独立思考与
高考全关注 | 从英语“七选五”题的蒙题到“可选性错排”问题的探究

高考全关注 | 从英语“七选五”题的蒙题到“可选性错排”问题的探究

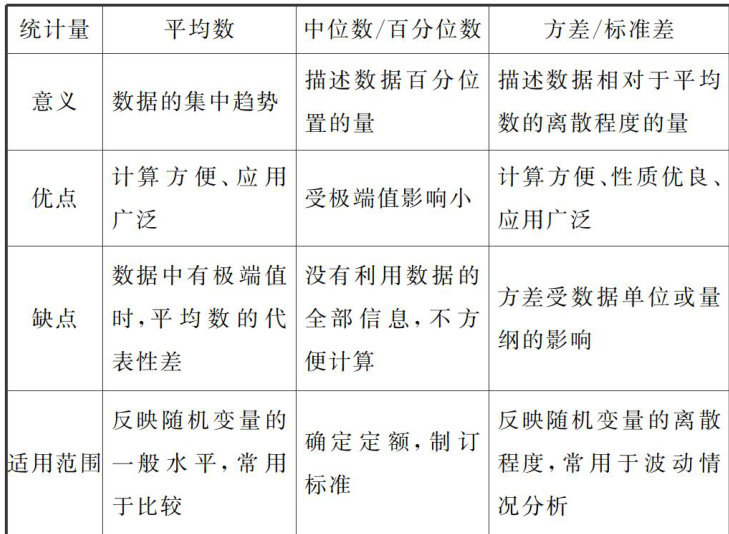
1 问题的提出高考英语中有一类叫“七选五"的试题，这类题是给出一篇缺少5个句子的文章，要求从文后的7个选项中选出5个最佳选项填入文中相应空缺处，使文章完整、连贯通顺.
高考全关注 | 统计量的比较与分析研究

高考全关注 | 统计量的比较与分析研究

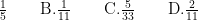
借助统计与概率知识解决现实生活中的开放性问题，是近年北京高考中常见的创新应用题型.此类题目背景多样，但核心均是对给定数据进行处理与分析，并依据统计与概率知识得出正确结论.本文旨在对常见统计量进行比较分析，并强调在阐述理由时，应紧扣数据分析结果，做到言之有据、逻辑严谨、表达准确.
高考全关注 | 例析以立体图形为背景的概率问题

高考全关注 | 例析以立体图形为背景的概率问题

纵览历年数学高考试题，不难发现当今新高考命题已发生了微妙的变化，由原来的“知识立意"转变为“能力立意”，在知识的交会点上命题已成为高考命题的“常态”基于此，以立体图形为背景的概率问题应运而生，这类问题将立体几何、排列组合和概率融合在一起，考查考生的数学能力和综合素养.下面举例加以说明.
高考全关注 | 空间几何体放置问题常见类型及策略突破

高考全关注 | 空间几何体放置问题常见类型及策略突破

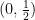
在高中数学课程体系中，立体儿何占据着重要地位，而空间几何体放置问题作为其中的关键内容，综合考查了学生的空间想象能力、逻辑推理能力和数学运算能力.这类问题形式多样、难度较大，学生在解题时往往感到困惑.根据《普通高中数学课程标准（2017年版2020年修订）》要求，立体几何部分需聚焦数学抽象、逻辑推理、直观想象等核心素养的培养，引导学生从空间视角认识事物的位置关系、形态变化和运动规律，强调通过对空间几
聚焦新课程 | 比赛中的概率问题探析

聚焦新课程 | 比赛中的概率问题探析

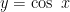
概率与统计是高中数学的重要内容.近几年，以比赛为背景的概率问题成为命题的热点，不但能让考生了解各种比赛的得分规则，而且能让考生“学以致用”，感受数学的应用价值.
聚焦新课程 | 探秘四类开放型问题

聚焦新课程 | 探秘四类开放型问题

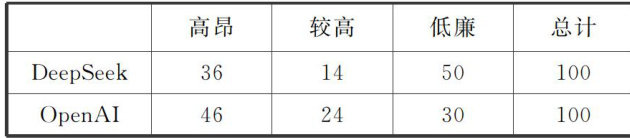
开放性试题能充分考查考生分析问题和解决问题的能力，因而备受命题者青睐.它可以分为条件开放型问题、结论开放型问题、条件和结论同时开放型问题等，每种题型的求解策略有所不同，笔者探讨常见的几类开放型问题
聚焦新课程 | 聚焦概率统计提升数学素养

聚焦新课程 | 聚焦概率统计提升数学素养

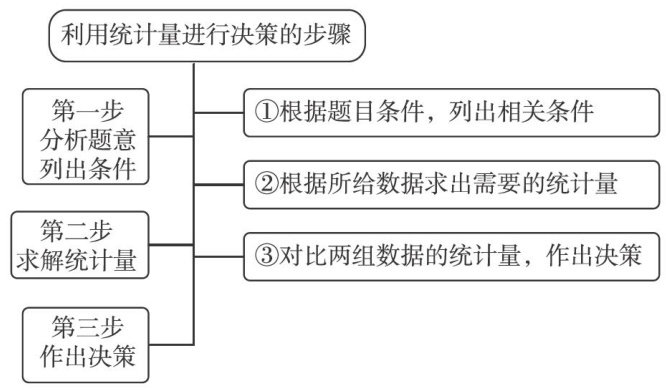
概率统计问题是近几年高考数学的热点题型，其综合性强、灵活度高.命题通常以现实生活为背景，着重考查学生运用数学知识解决实际问题的能力.求解这类问题，学生需从题目中提取关键信息，运用所学概率知识分析数据特征，发现问题规律，进而建模分析问题.本文剖析近儿年高考重点考查的热点题型，为读者提供参考.
聚焦新课程 | 利用统计量进行决策

聚焦新课程 | 利用统计量进行决策

在现实生活中，有时需要根据数据进行决策.例如，企业在选择原材料供应商时，需依据不同供应商提供的产品质量数据进行抉择；学校在评估学生成绩时，要考虑成绩的整体水平与波动情况.统计量作为描述数据特征的重要工具，在这些决策过程中发挥着关键作用.平均数和方差是众多统计量中极为重要的两个统计量，平均数能反映数据的集中趋势，让我们了解数据的一般水平；方差则体现数据的离散程度，帮助我们知晓数据的稳定性.掌握利用平
题根研究 | 对课本一道习题的多维度探究

题根研究 | 对课本一道习题的多维度探究

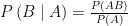
在概率论教学中，随机游走模型是理解二项分布、组合计数和随机过程的重要载体.本文以一道经典的课本题目（例1）为例进行多维度探究.
考题分类评析 | 条件概率题解法探究

考题分类评析 | 条件概率题解法探究

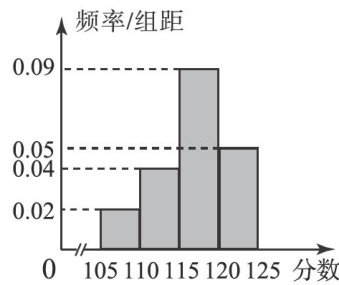
求实际问题中的条件概率是考试中常见的一类题型，求解这类问题有多种方法，如定义法、古典概率基本事件法、缩减样本空间法、概率性质法、全概率公式法等，本文结合例题加以探究.
考题分类评析 | 直击独立性检验热点题型

考题分类评析 | 直击独立性检验热点题型

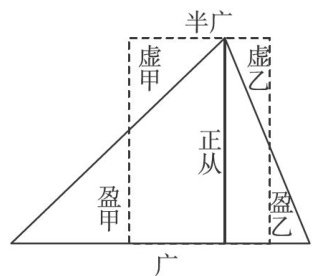
独立性检验是统计中的重要知识点之一，它可以判断两个分类变量之间是否显著具有某种关联性.虽然其内容比较简单，但往往与概率统计中的其他知识交会，具有一定的综合性.那么它通常与哪些知识交会呢？本文列举两种热点题型加以分析探讨.
考题分类评析 | 几何图形中的计数问题探究

考题分类评析 | 几何图形中的计数问题探究

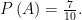
几何图形中的计数问题是高中数学各级各类考试中较为常见的一类问题，主要考查两个计数原理和排列组合知识与方法的灵活应用，本文探究这类问题的求解策略，
考题分类评析 | 用列举法求解概率中的一类问题

考题分类评析 | 用列举法求解概率中的一类问题

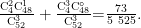
列举法是求解概率问题的常用方法，尤其适用于求解一些较为复杂的古典概型问题.当概率问题中样本空间中的样本点较少或样本点呈现出一定规律时，列举法是首选.如何将样本点一一列举，并做到不重不漏呢？教材介绍了列举法的三种常见形式：枚举法、列表法和树状图法，本文举例说明.
重点辅导 | 关于二项分布与超几何分布的三个问题

重点辅导 | 关于二项分布与超几何分布的三个问题

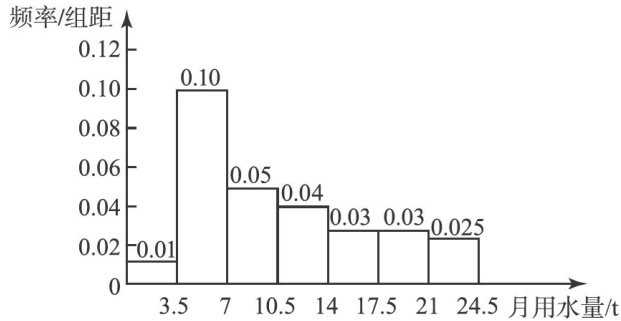
二项分布与超几何分布是两个重要的概率模型，诸多涉及概率判断的问题均可借助这两个概率模型加以解决，由于其应用广泛，故常出现在各类考试中.但这两个概念比较容易混淆，由此可能造成误判和错解，所以透彻理解并正确区分这两个概率模型至关重要.本文对这两类概率分布进行比较与辨析，供参考.
重点辅导 | 例谈统计图表的数据分析与应用

重点辅导 | 例谈统计图表的数据分析与应用

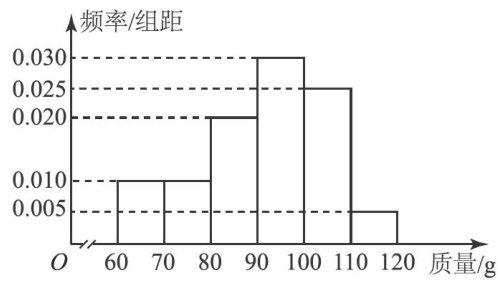
在现实生活中，统计问题常常以图表的形式展现，直观形象，让读者一目了然.高考中统计试题常考查考生的识图能力、用图能力和数据分析能力，那么常用的统计图表有哪些呢？如何分析与应用这些图表中的数据呢？本文举例说明.
重点辅导 | 直击概率与统计中的决策问题

重点辅导 | 直击概率与统计中的决策问题

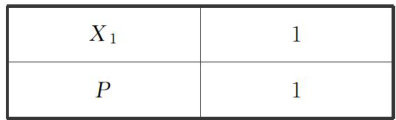
概率与统计是高中数学的重要内容，也是高考命题的重要考点，考查考生数据分析和数学建模等核心素养.学以致用，是新高考命题的重要原则之一，而利用概率与统计的知识对生活中的某些问题进行决策，正与之契合.这类问题主要有哪些呢？笔者结合典例进行探讨.
重点辅导 | 概率统计中的无分布列求期望问题研究

重点辅导 | 概率统计中的无分布列求期望问题研究

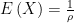
概率统计是高中数学的重点内容，近年来，随着对期望的深入考查，会出现随机变量无法列出所有可能取值的情形，导致期望无法计算.在这类问题中，已有学者提出建立递推关系式，将期望转化为数列求通项.该方法虽能奏效，但仍存在明显的不足：若递推关系式十分复杂，求数列通项将会十分困难.对于这个问题，笔者提出使用逐项期望累加法和全期望公式法，能在不使用递推关系的基础上回避求分布列，从而快速求期望.
难点挑战 | 三大概率分布的最可能成功次数及其应用

难点挑战 | 三大概率分布的最可能成功次数及其应用

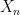
概率分布在统计学、物理学、经济学、信息技术、生物医学等多个学科领域中具有广泛的应用.二项分布、泊松分布和超几何分布作为三种常见的离散型概率分布，其最可能成功次数不仅是描述随机事件集中趋势的关键指标，还在跨学科的实际问题建模与推断中发挥着重要作用.研究最可能成功次数有助于深入理解不同概率分布的形态特征，为工业质量控制、风险评估、生物种群研究、数据科学等领域的概率推断提供理论支持.本文系统阐述三种分布
难点挑战 | 概率中的线性递推问题探究

难点挑战 | 概率中的线性递推问题探究

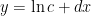
概率中的线性递推问题是概率与数列的综合问题，是新高考背景下的一个高频考点，对数学知识、能力与思维要求较高.本文以人教A版普通高中教科书数学选择性必修第三册91页第10题为例，探究一阶、二阶线性递推概率模型，剖析解题思路，形成一般解题策略，助力学生理解其数学本质、掌握其内核思想，提高学生分析和解决复杂概率问题的能力.
难点挑战 | 聚焦非线性回归模型

难点挑战 | 聚焦非线性回归模型

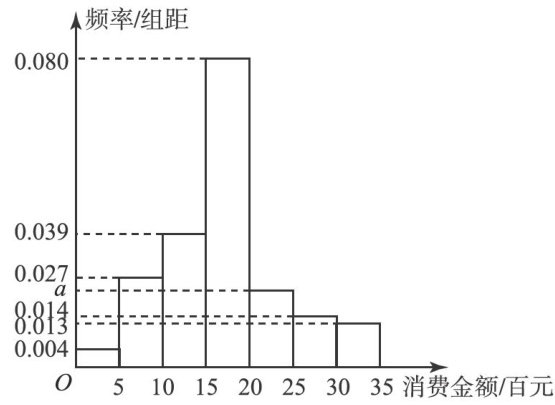
线性回归分析是指根据散点图位于某条直线附近的特征，利用最小二乘法求出直线方程，进而由线性方程中变量 y 与 x 之间的关系对未来进行预测.若散点图不具备线性回归的特征，该如何处理呢？本文介绍几个非线性回归模型及其应用，供参考.
难点挑战 | 独立性检验与统计概率综合问题探析

难点挑战 | 独立性检验与统计概率综合问题探析

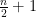
独立性检验在高考解答题中一般不会单独命题，通常以概率统计综合题的形式出现，以现实生活为背景，考查多个数学基础知识点及其应用，考查考生的数学建模、数据分析和数学运算的素养.独立性检验是如何与概率统计综合的呢？本文举例说明.
方法与技巧 | 二项式定理最值问题解题策略剖析

方法与技巧 | 二项式定理最值问题解题策略剖析

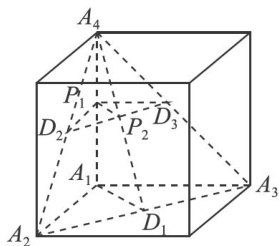
二项式定理最值问题综合了二项式展开式的通项公式、二项式系数的性质以及不等式求解等多方面知识，对学生的逻辑思维和运算能力要求较高.本文聚焦二项式定理最值问题，深入剖析不同题型，并总结有效的解题策略，旨在帮助学生深化对二项式定理的理解，提高数学学科核心素养.
方法与技巧 | 计数问题破解有招

方法与技巧 | 计数问题破解有招

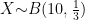
计数问题是高考中的常客，这类问题与实际生活联系紧密，题型多样，思路灵活，求解时首先要认真审题，弄清楚是排列问题、组合问题还是排列与组合综合问题；其次要抓住问题的本质特征，采用合理恰当的方法来处理.那么破解高考计数问题有哪些基本方法呢？让我们一起去探究。
方法与技巧 | 二项分布三类最值问题的解题策略

方法与技巧 | 二项分布三类最值问题的解题策略

在处理二项分布相关问题时，最值问题的求解常常是学生的难点.本文借助具体例题深人探讨二项分布中的三类最值问题，揭示如何巧妙运用数列、导数以及基本不等式等工具求解二项分布的最值问题
方法与技巧 | 概率题型梳理及其解题策略探究

方法与技巧 | 概率题型梳理及其解题策略探究

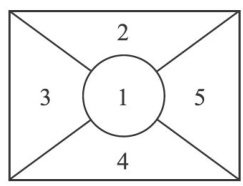
概率作为高中数学的核心模块，其知识体系与思维方法对学生数学核心素养的培养起着至关重要的作用.在《普通高中数学课程标准（2017年版2020年修订）》中，概率与统计是五大必修课程主题之一，在每年高考中均有考查，且呈现出题型稳定但情境创新的命题趋势.本文基于对高考真题的分析，围绕概率的考查形式展开探究，系统梳理题型并总结答题策略，旨在为高考备考提供指导.
学科防疫上 | 计数原理中的易错点分类剖析

学科防疫上 | 计数原理中的易错点分类剖析

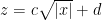
计数原理是高考必考内容，常以选择题、填空题的形式出现，考查难度不大，但易错点多.基于此，本文结合一些典型例题，对计数原理中的易错点进行分类剖析，为同学们备考提供一些参考.
数学建模与实践 | 上海滴水湖的湖底形状探究与三个岛屿体积估算

数学建模与实践 | 上海滴水湖的湖底形状探究与三个岛屿体积估算

对上海滴水湖的常规蓄水量与三个岛屿的体积进行估算，可为滴水湖的水资源管理与工程规划提供科学依据.本文基于上海滴水湖的地理与水文数据，首先证明了V形湖底、γ形湖底两种形态不适合滴水湖的情形；然后重点研究了锅形湖底、阶梯形湖底两种形态的适用性，分别给出了湖体体积估计与三个岛屿的体积估算.通过对湖底形状的数学建模与体积估算，结合旋转体体积的积分算法、分段函数拟合与约束优化算法，全面评估了不同湖底形态对湖
数学建模与实践 | 巧构示性函数，简化期望计算

数学建模与实践 | 巧构示性函数，简化期望计算

1 示性函数是什么

过往期刊

更多

猜你喜欢

泸州市图书馆电子阅览室