全部分类/
教育教学/
中学数学·高中版

中学数学·高中版

2024年04期

扫码免费借阅

目录

快速导航

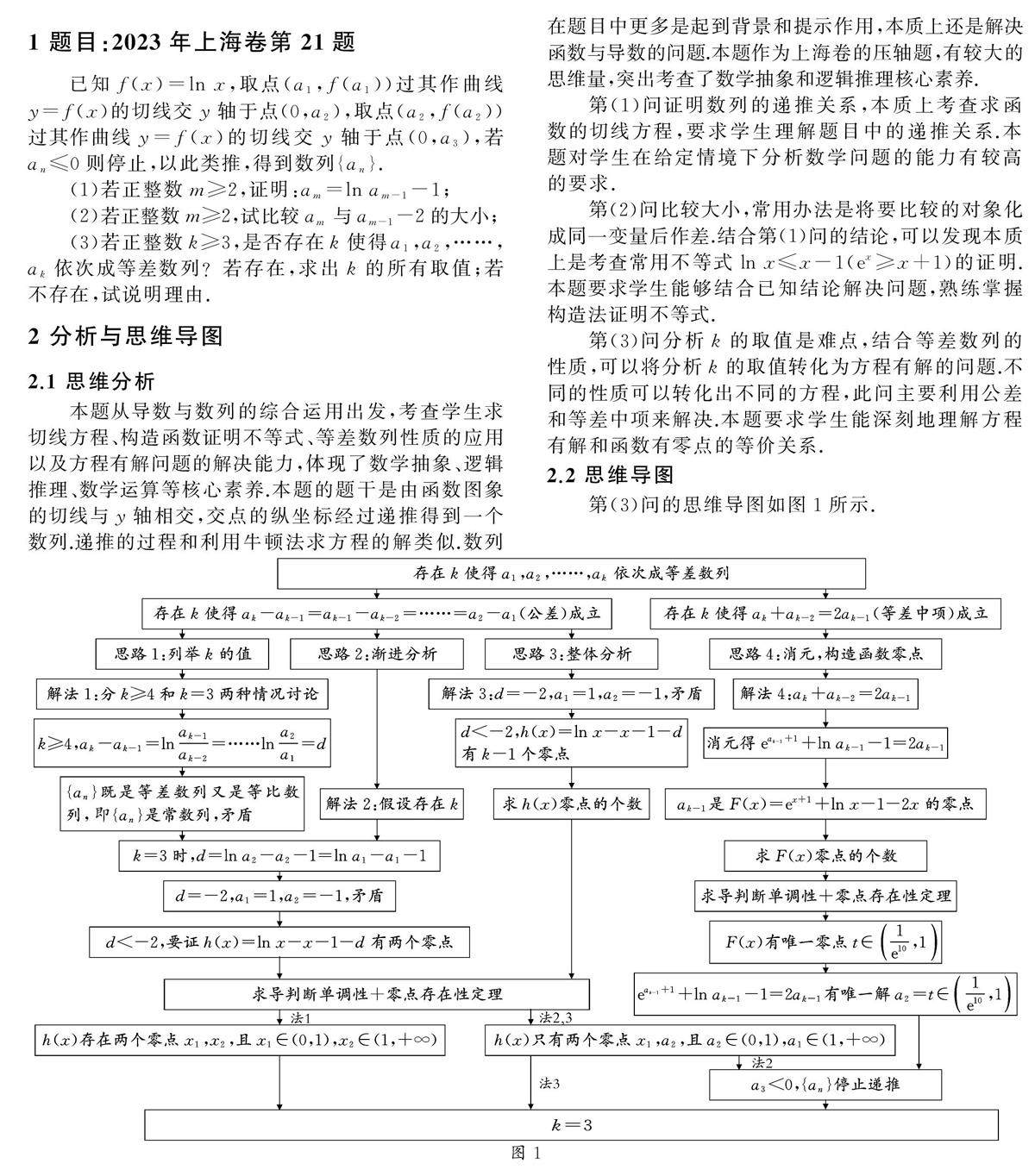
讲题比赛 | 揭示2023年上海卷第21题本质

讲题比赛 | 揭示2023年上海卷第21题本质

1 题目：2023年上海卷第21题已知f（x）=ln x，取点（a1，f（a1））过其作曲线y=f（x）的切线交y轴于点（0，a2），取点（a2，f（a2））过其作曲线y=f（x）的切线交y轴于点（0，a3），若an≤0则停止，以此类推，得到数列{an}. （1）若正整数m≥2，证明：am=ln am－1－1；（2）[JP3]若正整数m≥2，试比较am与am－1－2的大小；（3）若正
生态课堂 | 假以时间给你惊喜

生态课堂 | 假以时间给你惊喜

1 教学内容分析 1.1 内容分析本节课是由学生作业中的一道大题出发，追溯题目背景，是人教A版普通高中课程标准试验教科书数学21（选修）第73页A组第6题，第81页B组第3题. 通过圆锥曲线知识的学习，发现解决解析几何问题的通法——坐标法，偏重于相关量的数量关系的研究，由于代数运算复杂，对运算能力要求较高，往往使很多学生对解析几何望而生畏.事实上，解析几何问题的本质仍是几何问题，若能充分把
生态课堂 | 数学生态课堂视角下的高三复习课

生态课堂 | 数学生态课堂视角下的高三复习课

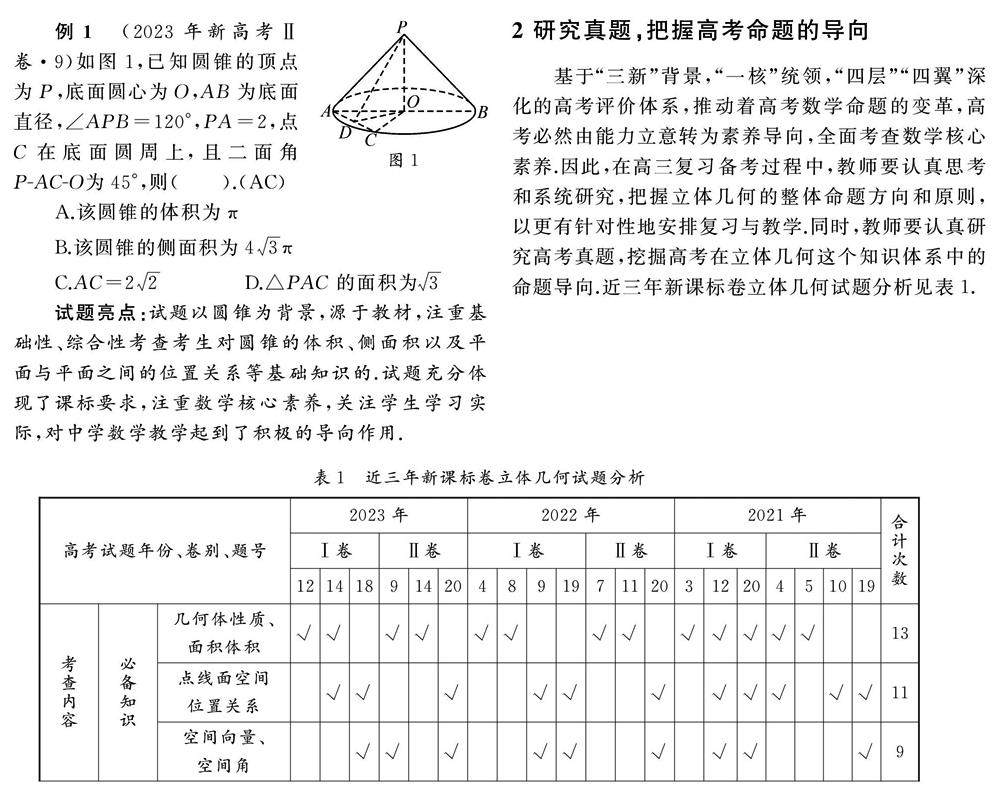
所谓数学生态课堂，就是课堂教学尊重学生的认知规律，尊重知识的发生、发展规律，同时还具有思想（主要是哲学思想，也包含数学思想）高度和文化厚度.两个尊重是教书，两个度是育人.高品位的数学课两个度不可少. 数学生态课堂在高三复习课中如何实施？两个尊重要求老师备课时要精心选题，在上课时要留充裕时间给学生做题.老师要精选三组题，第一组上课开始给学生做，第二组题是课堂例题，第三组题是课后作业.如果课堂不留时
教材点击 | 回归教材重基础精研真题提素养

教材点击 | 回归教材重基础精研真题提素养

高考立体几何试题的“四基”切入，落实对学生及数学基本能力、数学核心素养等方面的考查.基于此，新课标下的立体几何的复习备考应该更加灵活、全面. 1 回归教材，建立完整的知识体系高中数学教材是全面落实数学课程体系的重要载体，是落实课程目标以及培养学生数学核心素养的重要教学资源.同时，教材中的一些典型例（习）题、相关栏目等，也是历年高考数学命题的一个重要素材. 教师可以有针对性地对一些典型例（习
教学研究 | 高中数学教育教学研究年度综述

教学研究 | 高中数学教育教学研究年度综述

摘要：2023年中国人民大学复印报刊资料《高中数学教与学》共转载论文176篇，论文来源期刊以及作者所属地域比较集中.通过转载论文围绕拔尖创新人才培养、数学教育中的德育和美育、数学文化与数学史等热点问题进行了梳理. 关键词：高中数学教育；研究热点；历史回顾；拔尖创新人才；五育并举；数学德育；数学美育；数学文化；数学史 1 统计分析 1.1 刊物转载情况概述 2023年度《复印报刊资料＼5高中
教学研究 | 信息技术与高中数学深度融合的教学设计

教学研究 | 信息技术与高中数学深度融合的教学设计

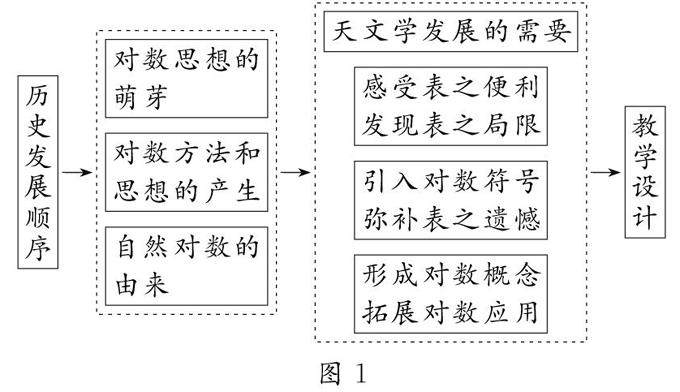
摘要：信息技术与数学教学深度融合己大势所趋，但在实际操作过程中，仍存在偏颇.基于此，以“正弦函数、余弦函数的图象”第一课时为例，从教学准备、课题引入、问题探究、回顾反思等环节展开了详细阐述，以实现信息技术运用的自然合理. 关键词：信息技术；正弦函数图象；余弦函数图象；深度融合；教学设计 1 教学准备 1.1 解读课程标准，深入分析教材新人教A版高中数学教科书必修第一册第五章“三角函数”单
教学研究 | 以史为鉴，重构课堂

教学研究 | 以史为鉴，重构课堂

1 问题提出《普通高中数学课程标准（2017年版2020年修订）》在课程结构中明晰了“数学文化融入课程内容”的要求，阐明了“数学的思想、精神、语言、方法、观点，以及它们的形成和发展”是数学文化的重要内容. “指数函数与对数函数”是高中数学教学的核心内容之一.课标要求“收集、阅读对数概念的形成与发展的历史资料，撰写小论文，论述对数发明的过程以及对数对简化运算的作用”等不作为考试内容的要求.人教
教学研究 | 大概念视域下课堂例题教学的实践

教学研究 | 大概念视域下课堂例题教学的实践

课堂教学是形成与发展学生数学核心素养的一个重要载体，更是落实课改理念的一个重要环节，因而课堂成为大概念视域下教学实践的一个重要场所. 重视课堂例题教学是在当前习题操作模块的基础上，合理引导学生积极主动参与其中，动口、动手、动脑，在课堂例题的基础上进行合理的深度学习，以典型例题为中心向外延伸与拓展，形成更加高阶的数学思维能力，促进课堂合理转型. 1 高考真题（2023年新高考Ⅱ卷·13）已知
教学研究 | 站在逻辑推理核心素养下，看解题路上的独特风景

教学研究 | 站在逻辑推理核心素养下，看解题路上的独特风景

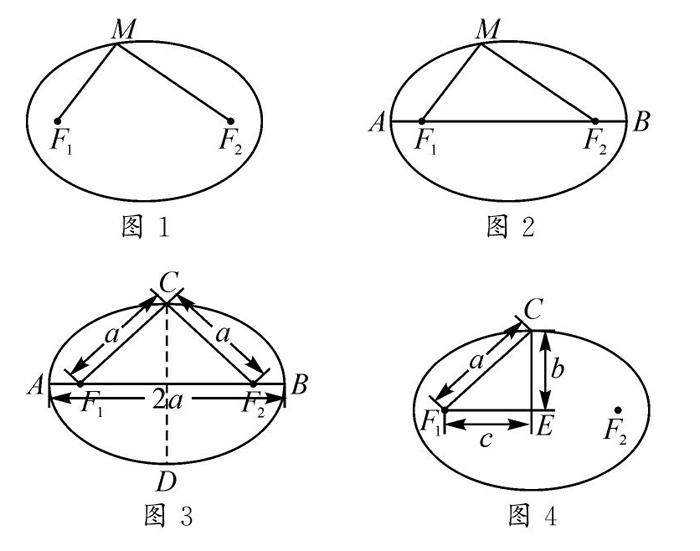
纵观历年各个地区的模拟题和高考题，解析几何一直是高中数学的难点所在，突出对逻辑推理、数学运算等核心素养的考查，通常计算量都比较大，学生往往望题兴叹.而学生的逻辑推理素养和数学运算素养皆为高中数学的核心素养，也是高考选拔功能的最佳体现.因此教师有必要、也必须要帮助学生突破此问题，从而培养逻辑推理和数学运算素养. 3 几点思考（1）注重基础，强调结构动直线过定点问题是解析几何的一个特殊问题，
教学研究 | 以“圆锥曲线”教学为例谈数形结合思想的渗透

教学研究 | 以“圆锥曲线”教学为例谈数形结合思想的渗透

摘要：数形结合既是一种数学思想方法，也是一种解题策略，是沟通数与形的桥梁，连接具体与抽象的纽带.本文中以“圆锥曲线”相关内容的教学为例，充分展示了数形结合在加强基础知识理解、提高学生解题能力、发展学生数学思维能力和数学能力等方面的优势，以期在日常教学中，通过合理有效的渗透，实现个体认知结构的优化和解题能力的提升，促进学生的全面发展. 关键词：数形结合；思维能力；数学能力数形结合将抽象思维转化
教学研究 | 发展高阶思维，推动深度学习

教学研究 | 发展高阶思维，推动深度学习

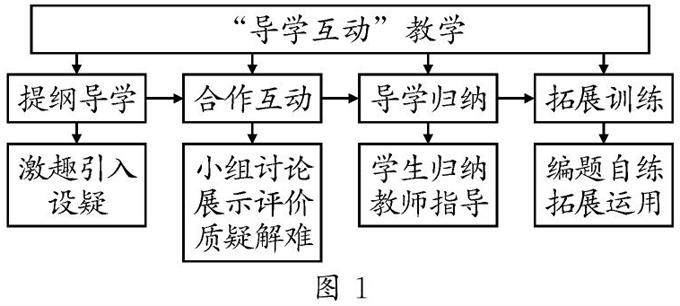
在新教材、新课程、新高考的“三新”背景下，依托当今日益复杂和快速变化的纷繁世界，高中数学课程更加注重数学学科知识与交汇知识的发生与发展的过程，关注并发展学生的思维，特别是高阶思维，借助分析、综合、创造与评价等方面心智活动，依托高阶思维所具备的更深入、全面分析和解决问题的能力，促进并推动深度学习，构建终身学习的基础. 1 合理变式拓展发展高阶思维，引导深度学习在数学课堂教学与学习过程中，教师要
教学研究 | 导学互动模式在高中数学教学中的应用

教学研究 | 导学互动模式在高中数学教学中的应用

在新课改的背景之下，极具高效性和科学性的高中数学导学互动教学模式正在被广泛运用.该模式是一种以学生为主体，教师与学生之间进行互动合作的教学方式[1].在该模式下，教师的角色发生了极大的改变，他们不再是知识的构筑师，而是承担起了引导的职责，通过设疑提问、引导讨论、合作探究等方式，培养学生的学习能力，让学生自主完成知识的构筑过程. 1 导学互动模式的应用原则 1.1 提高学生主动参与性导学互动
教学研究 | 高中数学建模素养培养存在的问题及对策

教学研究 | 高中数学建模素养培养存在的问题及对策

1 问题的提出我国在数学学科核心素养方面的研究取得了很多喜人的成果，如中国学生代表队在各类国际数学比赛中摘冠夺银.但在这些数学教育成就的背后，也隐藏着很多我们不得不承认的缺点或问题，比如我们的学生适合解决一些指向性明确的或者纯数学类的问题，对于生活化的问题往往束手无策.针对该现象，新课改指出了“数学建模”是学科核心素养和解决问题的基本方法之一，对于提高学生的数学知识应用能力有着极佳的效果.笔者
教学导航 | 重视概念教学提升核心素养

教学导航 | 重视概念教学提升核心素养

摘要：本文中基于《普通高中数学课程标准（2017年版）》中阐述的在学生学习数学和应用数学的过程中，学生能发展数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等数学学科核心素养，以人教A版选择性必修第一册“2.1倾斜角和斜率”概念课为例进行教学设计.数学概念是数学的灵魂，概念教学一是要抓住概念的“质”（概念的内涵），二是要抓住概念的“量”（概念的外延），在此基础上培养学生的核心素养. 关
教学导航 | 立足经验生长辅以技术支持

教学导航 | 立足经验生长辅以技术支持

摘要：为了使学生通过数学课程的学习，获得基本活动经验的自然生长，本文中从学生的角度出发，通过GeoGebra的应用，对圆锥曲线“离心率和渐近线”教学进行整合设计，尊重学生的知识生成，使学生亲身经历数学探究过程，成为课堂真正的“主角”. 关键词：经验生长；信息技术；圆锥曲线；几何性质对于圆锥曲线的教学，人教A版教科书类比初等函数，“同构”研究方法、内容和过程，形成如图1所示的研究流程. 教科
教学导航 | 单元复习学案，创新主题设计

教学导航 | 单元复习学案，创新主题设计

在“新教材、新课标、新高考”的“三新”背景下，复数的单元复习教学设计，可以基于学案形式，借助创新主题设计，侧重于“四基”层面，合理创设知识网络与体系，掌握复数概念的基础性，凸显复数运算公式的应用性，拓展数学思维的灵活性，有效进行单元复习学案教学设计与安排. 复数的复习提升课，针对这一单元进行合理的复习学案设计，构造一个创新完美的形式.具体单元复习学案设计分为以下五个部分：知识网络、知识要点、主题
案例赏析 | 基于UbD理论的“数列”单元教学设计

案例赏析 | 基于UbD理论的“数列”单元教学设计

摘要：文章基于UbD理论的基本思想，制定了理论下的逆向单元教学设计框架，即要素分析、确定预期结果、确定合适的评估证据、设计学习体验四个阶段.以人教A版选择性必修第二册“数列”单元为例，进行单元设计，致力于促进学生深层次理解知识，把握数列的本质，提升学生核心素养. 关键词：UbD理论；数列；单元教学设计 UbD理论是追求理解的逆向教学设计，由格兰特和杰伊提出，“逆向”体现在将教学评价置于教学活动
案例赏析 | “三角函数的概念”教学实录与思考

案例赏析 | “三角函数的概念”教学实录与思考

“三角函数的概念”是人教A版（2019年）必修第一册第五章第二节的内容.本节课的内容起着承上启下的作用，承接初中阶段的锐角三角函数和高一阶段第一章集合的内容，为学生后续学习三角函数的恒等变换、三角函数的图象与性质等内容作铺垫，同时又渗透了数形结合、转化与化归的数学思想，培养学生的抽象能力、建模能力以及利用信息技术解决实际问题的能力.近期，笔者在内蒙古赤峰市S中学见习，观摩了A教师一节“三角函数的概
案例赏析 | 基于数学核心素养的高中数学概念教学

案例赏析 | 基于数学核心素养的高中数学概念教学

摘要：数学概念是构成数学知识的基础，是解决数学问题的前提.在新高考背景下，教师要重视概念教学与数学核心素养的融合，通过创设情境引导学生经历概念形成、深化等过程，让学生在独立思考与合作探究中把握数学概念本质，提高学生分析和解决问题的能力，提升学生数学核心素养. 关键词：数学概念；概念本质；数学核心素养数学概念课是最重要的，也是最难上的.之所以说数学概念课重要，是因为数学概念是构成数学知识体系的
案例赏析 | 渗透数学文化提升数学素养

案例赏析 | 渗透数学文化提升数学素养

数学教学不单是知识与技能的教学，更是精神和文化的教学.不过在传统数学教学中，课堂教学只注意数学技能与知识的传授与灌输，完全忽视数学文化的渗透，课堂氛围枯燥乏味，大大降低了学生参与课堂的积极性，影响教学效果和学习品质.新时代背景下，我国教育领域对数学文化及数学素养的认识逐步加深，数学教学逐渐由“数学知识与技能的教学”走向“数学文化的教学”[1].教学中教师不断更新教学理念、转变学生的学习方式，让数学
案例赏析 | 指向思维能力的数学情境创设

案例赏析 | 指向思维能力的数学情境创设

“课标”指出数学教学要培养学生发现、提出、分析和解决问题的能力，即提升学生的思维能力.问题是思维活动的载体，情境创设是问题生成的背景和基础，教师在情境中设计问题，使学生在新颖独特、科学合理的情境中进行探究，学会分析和解决问题，从而激活思维，深化对数学的理解.本文中从培养学生思维品质的角度，谈一谈在教学中有效创设教学情境的策略，供大家参考交流. 1 营造数学文化情境，促进学生深度思考数学文化是
学生培养 | 高中生数学运算素养的培养情况及提升策略

学生培养 | 高中生数学运算素养的培养情况及提升策略

摘要：数学运算素养是高中数学学科六大核心素养之一，是学生认识、理解、解决数学问题的重要工具，提升高中生数学运算素养具有重要意义.文章基于对高中生数学运算素养的培养情况分析，得出高中生在数学运算素养方面存在的问题，以“椭圆”知识为例，结合高中数学教学实际，提出高中生数学运算素养的提升策略. 关键词：核心素养；高中数学；数学运算素养 1 引言在《普通高中数学课程标准（2017年版2020年修订
学习指导 | 知根溯源守通求妙思变拓展

学习指导 | 知根溯源守通求妙思变拓展

深度学习是机器学习的一种，是一个源于人工神经网络的研究的基本概念，更是实现人工智能的必经路径.而在数学教学与学习过程中，学生主要通过数学的概念、公式、公理、定理以及性质等的学习，结合解题研究，从数学知识的浅显理解走向深刻掌握，发展核心素养，这其实也是一个数学深度学习的过程，是数学教学与解题研究应追求的一种理想状态. 1 知根溯源知根溯源，回归数学问题的本质与根源，挖掘数学问题的题意内涵与本源
学习指导 | 抽象函数周期性学习的“四境界”

学习指导 | 抽象函数周期性学习的“四境界”

抽象函数问题是近年来高考命题的热点，因为它既能反映数学的本质特征，又能体现新课标对数学抽象和逻辑推理等核心素养考查的要求.在对抽象函数性质的考查中，特别是周期性问题比较隐蔽，很难把握，在学习中不少学生只见树木，不见森林，很有畏难情绪，甚至部分教师在教学中也是蜻蜓点水，浅尝辄止.本文中将周期性的深度学习分为“四个境界”，层层递进，结合近年来高考试题对此进行剖析，供读者参考. 5 总结周期性的学
试卷评析 | 删繁就简三秋树，领异标新二月花

试卷评析 | 删繁就简三秋树，领异标新二月花

摘要：分析2023年数学新高考Ⅰ卷，发现题型和难度相对稳定.新高考试题简洁明了，考查学生基础知识的同时重视学生关键能力的探求.本文中通过整体试卷评析、部分试题评析及近三年全国卷对比评析三个板块对2023年新高考Ⅰ卷进行评价. 关键词：新高考Ⅰ卷；试题分析；试卷评析 1 综述 2023年教学新高考Ⅰ卷严格依据高中课程和高中课程评价体系，深化基础性和综合性，注重数学运算［1］.试题简洁明了，体现
命题历程 | 原创函数与导数解答题的一次实践

命题历程 | 原创函数与导数解答题的一次实践

1 题目 2 命题过程 3 试题分析以及思维导图 4 测试结果及分析 4.1 测试对象为调查本题编制质量，难度设置是否适宜，是否具有良好的区分度，将本题编为“高三数学周练8”中的第21题，对本校高三学生其中一平台53人，二平台48人，共101人进行了书面测试.此次书面测试共发放101份，收回101份，回收率100%. 5 命题体会与反思 5.1 命题体会本次命题的考查范围是函数
试题研究 | 开阔思路，寻求多解

试题研究 | 开阔思路，寻求多解

摘要：立体几何的综合题经常涉及到多面体的几何特征与动态问题，能够全面有效地考查考生对所学内容灵活应用的能力，因此一直是高考的热点，也是分值较高、难度较大的压轴题型之一.本文中通过对高考真题的解析探究、变式演练和方法总结，探索这类题型的多种解题思路与方法. 关键词：真题再现；解法探究；思路分析；变式演练；方法总结立体几何的综合题主要分为两类：一类是空间线面关系的判定和推理论证.高考中对该部分内
试题研究 | 借助“一题多解”，倡导“一题多变”

试题研究 | 借助“一题多解”，倡导“一题多变”

作为高中数学中的一个重要知识点与基本解题工具，平面向量凭借自身同时兼备“数”的基本属性与“形”的结构特征这一内涵，成为高中数学中一道特殊的亮丽风景线. 在实际数学试题的命制与解题过程中，往往可以从“数”与“形”这两个不同的视角加以切入与应用，丰富问题的内涵与实质，也为问题的解决提供更加多样变化的视角，体现创新性与应用性. 4 教学启示 4.1 “数”“形”结合，开拓思维平面向量集“数”“
试题研究 | “动”“静”结合，“形”“数”转化

试题研究 | “动”“静”结合，“形”“数”转化

平面解析几何中的取值范围问题，是高考数学试卷中一个熟悉的“面孔”，难度中等.此类问题可以综合点、直线、圆、圆锥曲线等相关元素，合理交汇其他相关知识，形式新颖，背景生动，“动”“静”结合，融合度高，可以出现在选择题或填空题中，也可以出现在解答题中，变化多端，形式各样，能很好考查学生的数学知识、数学思想方法与数学能力，充分体现试题的选拔性与区分度，备受各级各类考试命题者的青睐. 4 教学启示 4.
解法探究 | 巧用分段放缩法证明函数不等式

解法探究 | 巧用分段放缩法证明函数不等式

摘要：放缩法是证明函数不等式的一种常见方法，如寻找中间常量、切线放缩、割线放缩、利用泰勒展开式放缩等，但放缩的尺度不易掌握．分段放缩法将函数不等式成立的区间划分为若干个子区间，有利于在每个子区间上缩小放缩的幅度，避免“放过头”的问题，从而证明函数不等式在整个区间内成立．本文中通过几个实例，剖析了分段放缩证明函数不等式的方法，以及如何调整区间的划分，对函数不等式的证明是一个很好的补充．关键词：函
解法探究 | 由一道解析几何题引发的一题多解与多题归一

解法探究 | 由一道解析几何题引发的一题多解与多题归一

摘要：解析几何是高考数学考查的重点内容，其中定点、定值问题也是高考的常考问题.解决此类问题常用的方法主要有两类.一类是直接从已知条件出发，利用韦达定理求解；还有一类是先猜后证，通过特殊情况确定定点或定值，再用常规方法解决.本文中以一道解析几何题为例，通过一题多解再到多题归一，培养学生的发散思维能力与归纳总结能力，进一步提升学生的数学学科素养. 关键词：定点；定值；韦达定理近几年高考中经常考查
解法探究 | 运用一题多变探究与n2有关的数列求和问题

解法探究 | 运用一题多变探究与n2有关的数列求和问题

摘要：一题多变可以很好地培养学生的数学思维，通过探究与n2有关的数列求和问题，给出一题多变在设计时需要注意体现整体性和层次性，从而为一题多变的教学提供一定的参考. 关键词：一题多变；数列求和在数列的学习中，经常会遇到与等差数列有关的求和问题，如对形如an=n+2n，an=n·2n，an=1n（n+1），an=（－1）n·n的数列求和时，一般分别采用分组求和法、错位相减法、裂项相消法、并项求和
教学感悟 | 提高习题训练实效提升学生数学素养

教学感悟 | 提高习题训练实效提升学生数学素养

摘要：谈起数学教学就不得不谈数学练习，它是巩固学生基础知识，提升学生思维能力的必经之路.在具体练习中，教师要紧抓专题练习，通过变式训练、梯度练习、纵横拓展等方式将相同或相似的知识进行反复的练习，以此巩固“双基”，落实数学素养，提高学生数学综合应用能力. 关键词：数学练习；思维能力；数学素养在教学中，为了帮助学生巩固“双基”，深化思维，教师可以在一定的时间内引导学生对相同或相似的内容进行反复练
教学感悟 | 来路—思路—出路—套路，教学研题“四部曲”

教学感悟 | 来路—思路—出路—套路，教学研题“四部曲”

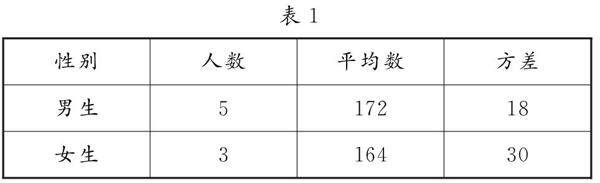
摘要：借助一道高考平面向量数量积的最值问题的求解，合理诠释数学问题解题研究过程中的“四部曲”——来路、思路、出路、套路，挖掘问题内涵与实质，总结解题规律，尝试为数学问题的求解与解题研究提供一个基本学习模板，指导数学教学与解题研究. 关键词：平面向量；数量积；最大值在数学课堂教学以及解题研究过程中，特别是在高考复习阶段，教师合理选取经典问题，多方位挖掘问题的内涵，尝试做到数学解题研究的“四部曲
教学感悟 | 基于统计知识，高三复习建议

教学感悟 | 基于统计知识，高三复习建议

《普通高中数学课程标准（2017年版2020年修订）》中多次出现“情境”一词，《中国高考评价体系》也规定了高考的考查载体——情境，并以此承载考查内容，实现考查要求.数学情境是高考评价体系中最重要的创新之一，是实现“价值引领、素养导向、能力为重、知识为基”的考查目标的载体.数学试题情境一般取材于学生生活中的真实问题，贴近学生实际，具有现实意义，具备研究价值. 对统计知识（包括必修第二册第九章“统计
教学感悟 | 解题教学培育学生数学思维能力的探索

教学感悟 | 解题教学培育学生数学思维能力的探索

俗语有云：“授人以鱼不如授人以渔.”数学教学是为了培养学生学习能力与生活能力的教学，教师的课堂引导对学生思维的发展具有深远的影响.在新课标的引领下，以核心素养为导向的数学教学，学生才是课堂真正意义上的主人，所有的教学活动应基于“以生为本”的基础开展[1].因此，高中数学教学不再是知识的传授那么简单，而应在充分理解课标要求与学情的基础上，借助课堂教学激趣启思、拓展学生的思维、挖掘潜能，促使每个学生都
教学感悟 | 基于数列知识，高三备考复习建议

教学感悟 | 基于数列知识，高三备考复习建议

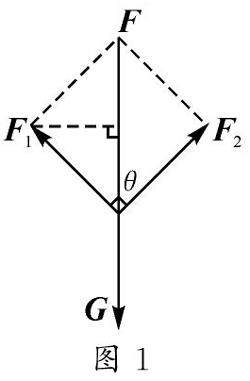
摘要：作为高考中的主干知识之一，“数列”模块的复习备考是高考复习中的一个重要环节.通过把握复习方向，强调数学运算，加强解题教学，强化主题研究等层面展开，剖析复习备考建议，全面提升数学能力与培养核心素养，优化复习备考效益. 关键词：数列；高考；备考；复习建议近几年的高考对数列知识的考查切实吻合《普通高中数学课程标准（2017年版2020年修订）》的要求.以数列的基本概念、基本类型、基本公式、基
争鸣探索 | 跨越抽象与现实边界:高中数学跨学科教学模式探索与实践

争鸣探索 | 跨越抽象与现实边界:高中数学跨学科教学模式探索与实践

摘要：跨学科教学有助于拓展数学思维，深化学习意识，形成知识体系，让学生以数学的方式理解生活、理解世界.本文中以新课程教育理念为基础，从学生创新思维、探究精神、数学能力发展等角度入手，概述了跨学科视角下高中数学教学实践路径，通过多学科知识交叉渗透与活动方案设计，培养学生数学创造思维和解决问题能力，提高数学素养与学习能力. 关键词：高中数学；跨学科教学；核心素养；学习能力新课标强调以培养学生的数
争鸣探索 | 浅析如何提升应用题教学质量促进解决问题能力提升

争鸣探索 | 浅析如何提升应用题教学质量促进解决问题能力提升

摘要：在新课改的推动下，数学教师对培养学生问题解决能力有了更为深刻和全面的认识，实现了从“解题”到“解决问题”的过渡.本文中分析了数学应用题教学普遍存在的问题，并提出了行之有效的教学策略，以此提升应用题教学质量，发展学生应用意识，促进学生解决问题能力全面提升. 关键词：解题；解决问题；策略在“功利”教学的影响下，分数是判断学习效果的唯一标准，为此，数学学习的目的就是让学生尽可能多地掌握数学知
争鸣探索 | 基于深度学习的概念课教学

争鸣探索 | 基于深度学习的概念课教学

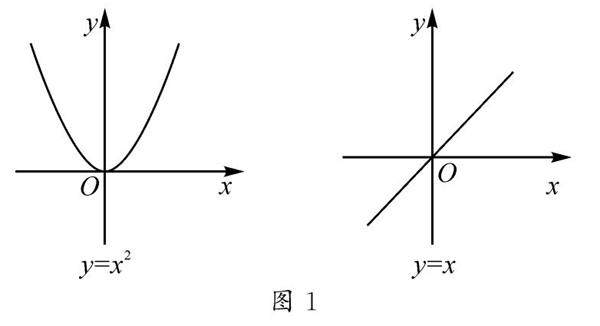
在新课标、新教材、新高考的“三新”背景下，课堂教学模式的优化显得更加重要.构建以学生的学为中心的课堂教学模式，从学生学的角度来设计“学历案”，从教材入手，剖析实质，挖掘内涵，深度学习，这更加符合人本主义学习理论，充分体现了高中数学课堂教学中以教师为主导、学生为主体的教学原则，合理构建起“教”与“学”之间的桥梁，还学生课堂的主体地位，给深度学习提供更加肥沃的土壤. 特别地，涉及数学中的概念课教学，
争鸣探索 | 构建有效提问优化数学课堂

争鸣探索 | 构建有效提问优化数学课堂

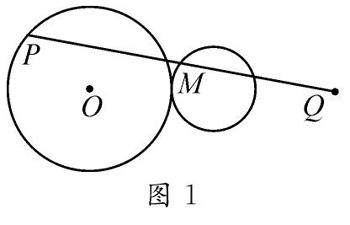
摘要：课堂提问在课堂教学中是必不可少的，它是激发学生学习热情，提升学生思维品质，提高教学效率的重要路径.有效提问可以引发学生思考，帮助学生主动获得知识，激发学生潜能，实现思维、能力的全面提升.本文中分析了课堂提问中存在的一些问题，并提出了几点有效策略，通过课堂提问的优化，促进学生综合能力和综合素养的全面提升. 关键词：课堂提问；有效提问；策略课堂提问是一门教学艺术，是一种重要的教学手段，是师
争鸣探索 | 发挥信息技术优势提升课堂教学效果

争鸣探索 | 发挥信息技术优势提升课堂教学效果

摘要：新课程改革的进一步深入，对高中数学的教学手段、教学方式等提出了全新的要求.将信息技术与高中数学教学相结合既能满足学生的发展需求，也符合新课改的要求，在发展学生思维、培养学生的创新意识、提升教学质量等方面发挥着重要的作用.本文中展示了几何画板在高中数学教学中的优势，以期通过适时、适度、适当的应用，提升课堂教学效果，实现学生的可持续发展. 关键词：信息技术；几何画板；教学效果数学是一门比较

过往期刊

更多

猜你喜欢

泸州市图书馆电子阅览室