全部分类/
教育教学/
中学数学·高中版

中学数学·高中版

2024年01期

扫码免费借阅

目录

快速导航

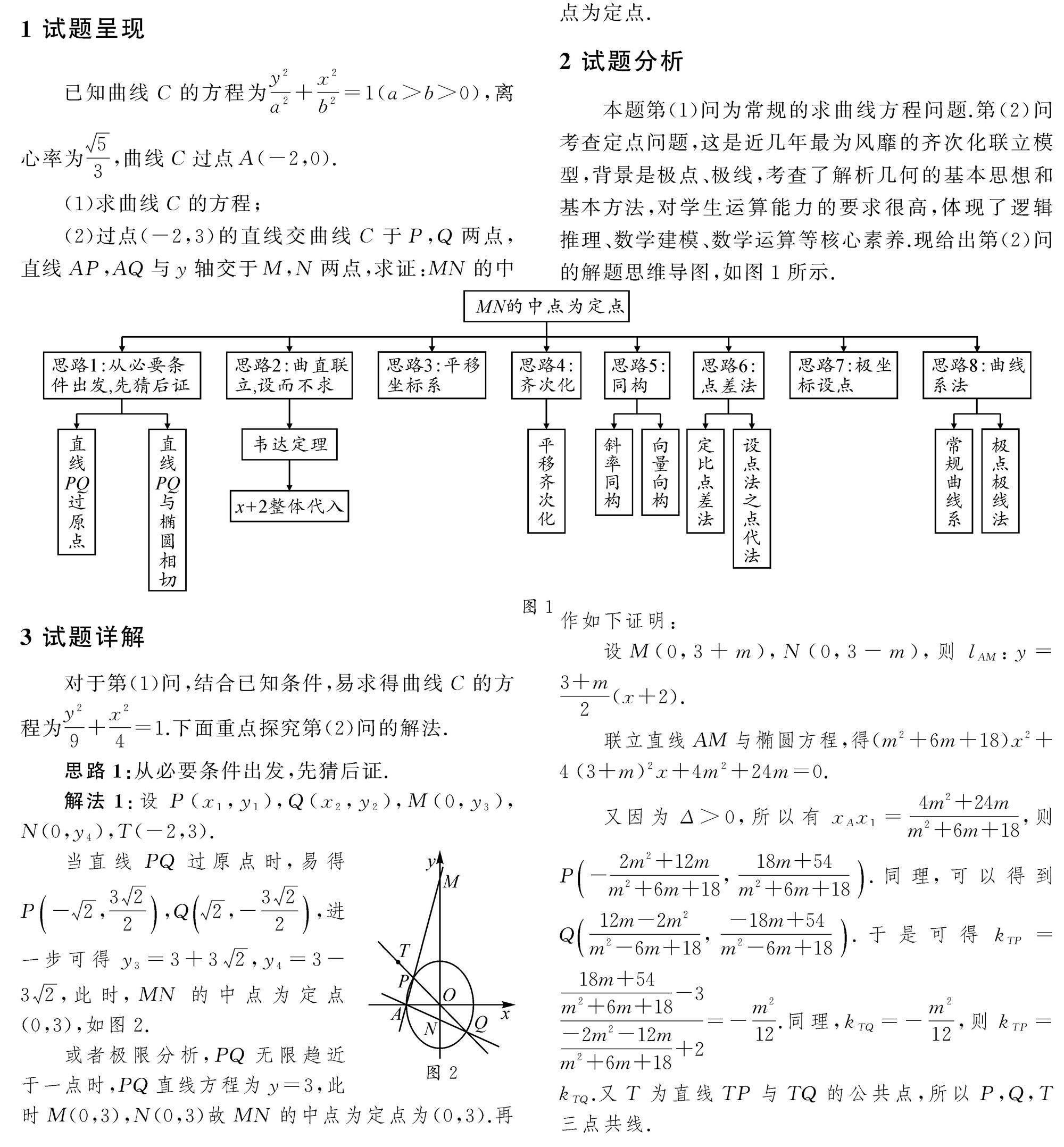
特色展台 | 直觉引领运算探究模型回归

特色展台 | 直觉引领运算探究模型回归

1 试题呈现已知曲线C的方程为y2a2+x2b2=1（a>b>0），离心率为53，曲线C过点A（－2，0）. （1）求曲线C的方程；（2）过点（－2，3）的直线交曲线C于P，Q两点，直线AP，AQ与y轴交于M，N两点，求证：MN的中点为定点. 2 试题分析本题第（1）问为常规的求曲线方程问题.第（2）问考查定点问题，这是近几年最为风靡的齐次化联立模型，背景是极点、极线，
课程视点 | 基于数学抽象的高中数学教材分析与比较

课程视点 | 基于数学抽象的高中数学教材分析与比较

摘要：数学抽象是高中阶段的六个数学学科核心素养之一.本文中从数学抽象的视角对人教A版教材和苏教版教材中“三角函数”一章的内容进行分析和比较，探寻教材落实发展学生数学抽象素养的要求以及两版教材在这一方面的区别，以期为教师教学提供参考. 关键词：数学抽象；人教A版；苏教版；三角函数 1 研究问题数学抽象主要包括从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系，从事物的具体背景中
课程视点 | 母题探源：拓展教材习题的价值

课程视点 | 母题探源：拓展教材习题的价值

摘要：从教材（教科书）的两个习题出发，整合出一个不等式链，探究其在数学“大题”中的应用价值.大单元统筹教材资源，帮助学生构建数学单元整体认知体系结构，着力突破教学重难点，提升数学核心素养. 关键词：母题；教材；不等式链数学教材（教科书）中的习题是学生学习数学的重要载体，具有基础性的重要地位.教材习题的设置看似简单，有些甚至显而易见，但它们具有良好的梯度与针对性，是教材编写专家集体智慧的结晶.
课程视点 | 真题追本溯源，回归教材本源

课程视点 | 真题追本溯源，回归教材本源

摘要：高中数学教材中的一些典型例（习）题，具有相关模块知识的典型性与应用，也一直是高考数学命题的基本源泉之一.结合一道三角函数求值的高考真题的追根溯源，挖掘根源所在，开拓解题思路，总结性质规律，合理回归教材并挖掘教材知识，有效指导数学教学与复习备考. 关键词：三角函数；公式；换元；教材；习题高中数学教材例（习）题往往是每年高考数学命题的一个重要脚本，回归教材本源，合理挖掘教材例（习）题的各个
教法探索 | HPM视角下“正弦定理”的教学

教法探索 | HPM视角下“正弦定理”的教学

课题信息：宿州市教育科学规划课题“HPM视角下高中数学教学创新设计的实践研究”，课题编号为JKY20211093. HPM是数学史与数学教育之间关系的简称，数学史融入数学教学是当下HPM研究的一个重要领域.在高中数学中，正弦定理是求解三角形的重要工具.在“正弦定理”的教学中，教师应该尝试多种不同的教学模式.翻开数学史料，笔者发现古人已经探索出多种不同的正弦定理的证明方法，有不少漂亮的证法有必要介
教法探索 | “微信+腾讯课堂+智慧平台”融合的线上互动教学模式探索

教法探索 | “微信+腾讯课堂+智慧平台”融合的线上互动教学模式探索

课题信息：甘肃省教育科学规划普通高中数学教改实验专项课题“‘函数的概念与性质、幂指对函数’单元教学设计与实施研究”，课题立项号为GS＼GHBZX0069. 摘要：以高中数学三角函数“任意角”一节为例，通过“微信+腾讯课堂+国家中小学智慧教育平台”的融合，介绍了多网络平台融合的线上互动教学的基本步骤.从课前准备、课中线上授课、课后反思总结三个阶段进行了详细分析. 关键词：微信群；腾讯课堂；国家中
教法探索 | 高一新生数学关键能力的养成策略

教法探索 | 高一新生数学关键能力的养成策略

课题信息：泰州市第十二期教学研究十二期教研一般立项课题“高一新生数学学习关键能力的培养策略研究”，课题立项编号为TZJYYB2019-057. 数学关键能力是我们在现实生活中工作与数学学习过程中，对应数学知识的积累与升华，数学方法的理解、掌握、应用和内化，以及利用数学的视角来发现、提出问题，并借助数学的思维来分析、解决问题的综合能力.融合高考评价体系的整体框架以及《普通高中数学课程标准（2017
教法探索 | 数学课堂有效对话的三点认识

教法探索 | 数学课堂有效对话的三点认识

课题信息：福建省教育科学“十四五”规划2021年度常规课题“中学数学素养立意教学的测评导向推进策略研究”，课题编号为FJJKZX21-576；2021年泉州市基础教育教学改革专项课题“指向数学应用能力提升的教学评一体化研究”，立项批准号为QJYKT2021-015. 随着时代的不断发展，个体的民主意识不断增强，对话慢慢成为解决人际问题与处理社会关系的有效途径.教即倾听，学即诉说.从某种意义上说，
教法探索 | “等差数列的前n项和公式”教学设计

教法探索 | “等差数列的前n项和公式”教学设计

摘要：“等差数列的前n项和公式”作为优秀课例参加了“全国第十届高中青年数学教师优秀课展示活动”，本文中按教学过程设计、教学设计策略、教学反思的顺序对本单元的教学设计逐一进行说明. 关键词：等差数列；前n项和公式；单元教学设计；问题驱动教学；数学情境；数学文化 “等差数列的前n项和公式”选自人教A版普通高中数学教科书选择性必修第二册第四章第4.2.2节，笔者是基于单元教学对本节课进行设计的，一共
教法探索 | 基于“四个理解”的“幂函数”教学设计

教法探索 | 基于“四个理解”的“幂函数”教学设计

摘要：幂函数是学生在高中阶段最先接触到的基本初等函数，为后续学习其他函数起到了示范性的作用.本文中基于“四个理解”角度对幂函数的教学目标、教学重难点、教学方法、教学过程进行了细致的解读. 关键词：四个理解；数学教学；幂函数章建跃博士在“中小学数学课程核心内容及其教学的研究”中提出：改进课堂教学需基于理解数学、理解学生、理解技术、理解教学实施＼.本文中在把握数学本质的同时，立足数学核心素养并
教法探索 | 发挥学生主体作用，助推学生深度学习

教法探索 | 发挥学生主体作用，助推学生深度学习

目前，数学教学中依然存在着程序化、形式化、碎片化的浅层学习方式，影响了学生学习能力的提升和思维能力的发展.为了帮助学生获得更好的学习效果，数学课堂上需要对数学知识的深度学习，以此提高学生学习层次，强化学生学习能力，建构知识体系，让学生获得可持续学习能力，促进终身学习目标的达成＼.笔者以“等比数列的前n项和”教学为例，谈谈自己对深度学习的一些认识，供参考. 1 教学过程 1.1 联系旧知，明晰方
教法探索 | 立足核心素养，构建教学评一致性课堂

教法探索 | 立足核心素养，构建教学评一致性课堂

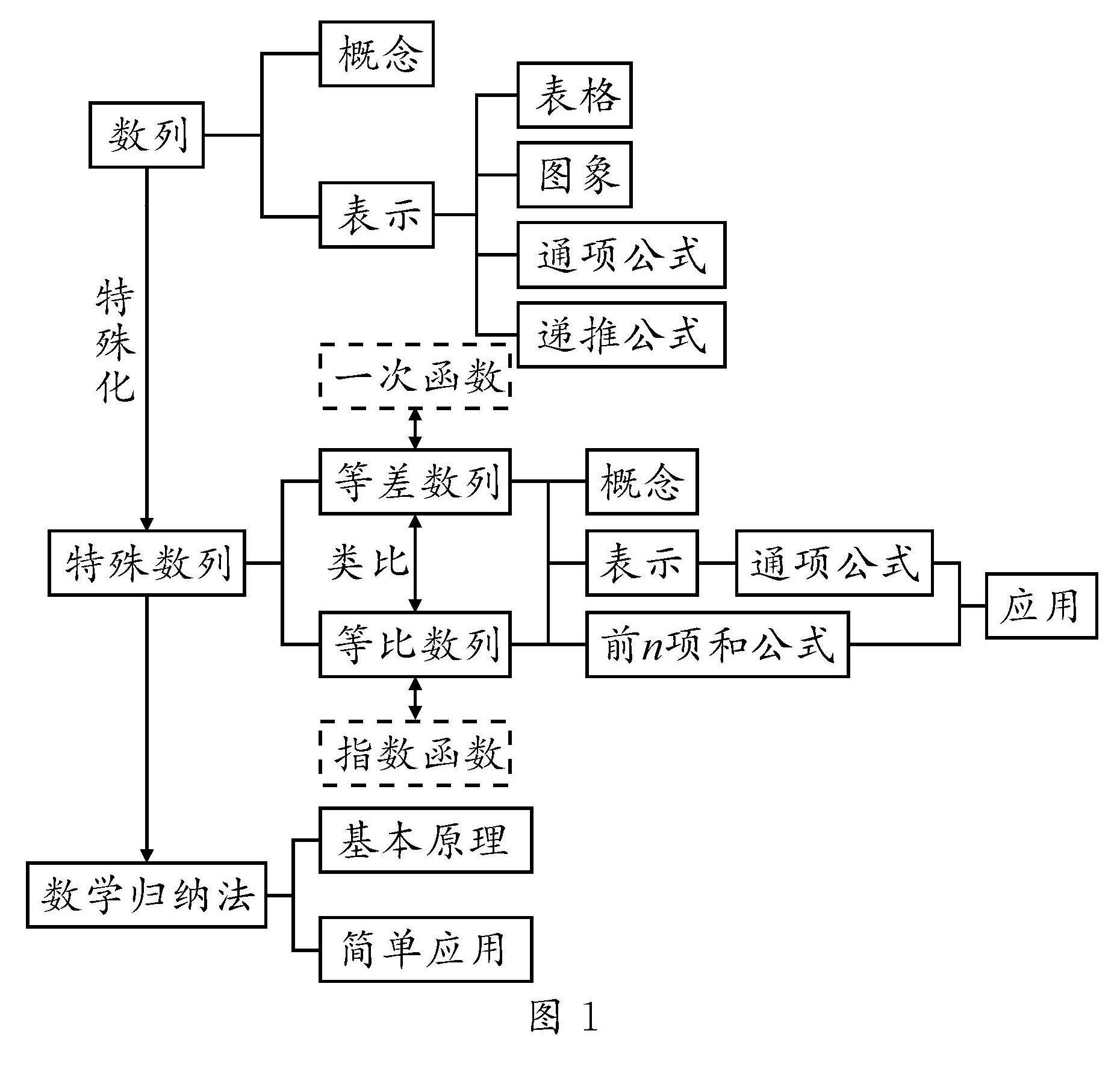
摘要：数学核心素养是学生在学习过程中逐渐形成的一种综合性运用知识解决问题的能力，培养学生数学核心素养是一个长期、反复、逐渐积累的过程.在实际教学中，教师应遵循教育规律，尊重学生认知水平，切实从教学实际出发设计符合学生认知规律的数学活动，让学生在活动中思考、感悟、提炼，以此构建教学评一致性课堂，促进学生数学核心素养的落实. 关键词：数学核心素养；数学活动；教学评一致性当下，培养学生数学核心素养
教法探索 | 重视教材体系，注重阅读理解，聚焦课堂教学

教法探索 | 重视教材体系，注重阅读理解，聚焦课堂教学

高考数学二轮备考复习是在一轮数学基础知识复习、验收与评价的基础上，主要以数学专题为主、相应“微专题”为辅，结合数学质检考试等形式来开展的，时间一般安排于次年元月初到四月初，主要以突破数学核心考点，提升数学关键能力为宗旨，丰富数学文化底蕴及数学解题思想和方法，目标是学会“解高考题”.为更好提升高考数学二轮备考复习效果，注重复习质量与效益，掌握下面的基本备考策略是必须也是必要的. 1 重视教材体系，
教法探索 | 利用“问题”驱动深度思考

教法探索 | 利用“问题”驱动深度思考

在一次高中数学同课异构教学研讨活动中，四位教师分别上了一节“统计”的起始课.四节课观摩下来，感觉教师风采各有千秋，但是四节课也存在两个共性问题.第一个问题是，没有关注起始课如何上.其中三位教师几乎是跳过章引言，直接进入第一课时的教学，没有站在更高的位置去设计教学，没有整体教学意识，只注重知识点的讲授.有一位教师虽然呈现了章引言，但是不尽人意，轻描淡写，一带而过.第二个问题是，所提问题启发性不强，没
教法探索 | 关注应用提升素养

教法探索 | 关注应用提升素养

基本不等式a+b2≥ab（a≥0，b≥0）是高考的一个重要考点，它在证明不等式与求函数最值中都有着重要的应用，它是一个值得深入研究的知识点.在基本不等式教学中，大多教师会从教学实际出发，设计符合学生认知的教学情境来激发学生探究的积极性，并提供时间和空间让学生经历公式的推导过程，以此让学生理解和掌握基本不等式.不过，学生虽然理解并掌握了基本不等式，但是在具体应用中还是会出现“一错再错”或“无从入手”
教法探索 | 借助同课异构提升教学效果

教法探索 | 借助同课异构提升教学效果

在一次教学调研活动中，笔者很荣幸地观摩了两节关于“函数的单调性”的公开课.两位执教者是来自于两所不同学校的优秀教师，他们有着不同的教学风格.通过对比和反思，笔者收获良多，这里与大家分享了一些教学细节，谈一些自己的看法，以期抛砖引玉. 1 教学实录 1.1 情境引入甲、乙两位教师都是把曲线图作为引入情境，试图借助图象让学生形成直观的认识.教师乙直接选择了教材案例——某天气温关于时间t的函数图
教法探索 | 合作交流让“教”与“学”更有效

教法探索 | 合作交流让“教”与“学”更有效

合作交流是课堂教学的一种重要教学形式，旨在通过师生和生生的有效互动让学生更好地理解知识，理解数学，激发学生数学学习兴趣.高中数学知识是抽象且复杂的，许多内容对思维要求较高，而学生的理解能力有限，这样学生在个别知识点的理解上难免会出现思维障碍，如果教学中教师能够为学生提供一个平等的、民主的学习环境，学生就可以积极表达自己的意见和见解.这样通过师生和生生的有效互动和交流，教师可以更好地了解学生、帮助学
学生学习 | 厘清运算对象与法则，探究运算思路和方法

学生学习 | 厘清运算对象与法则，探究运算思路和方法

数学运算是“新课标”中提出的数学六大核心素养之一.因此，数学运算在高考中受到了高度关注，“成也运算，败也运算”，几乎成为一种共识.从当下高中数学教学的现状来看，学生的数学运算能力在整体表现上依然比较“孱弱”，“一听就懂，一做就错”的现象普遍存在.采取切实有效的措施，使数学运算素养在课堂教学中落地生根，是一个值得我们高度重视的课题.下面以高考及其模拟试题中的“函数”问题为例，谈谈笔者的一些认识和体会
学生学习 | 促进学生问题提出的策略探究

学生学习 | 促进学生问题提出的策略探究

摘要：相比于问题解决，问题提出是一种更为主动的学习方式.如何提高学生问题提出的能力理应是教师考虑的重点，因此在波利亚的解题理论以及前人研究的基础上，本文中提出了几个针对提高学生问题提出意识和能力的策略. 关键词：问题提出；教学策略；波利亚解题理论数学问题的提出，本质上是提出对事物的本质属性、普遍联系和一般规律的疑问，通过数学抽象实现数学化，引入研究对象，明确研究内容和研究目标，是对“在一定条
学生学习 | 巧借坐标运算，妙解向量问题

学生学习 | 巧借坐标运算，妙解向量问题

摘要：利用坐标运算法解决平面向量问题是比较常见的一种技巧，也是解决平面向量中重点与难点问题的一大“法宝”.结合实例剖析，通过平面直角坐标系的构建与对应坐标的表示，合理数学运算，减少逻辑推理，实现平面向量解题的程序化运算处理，指导数学教学与解题研究. 关键词：平面向量；坐标；运算；数量积平面向量自身同时兼备“数”的基本属性与“形”的结构特征，是衔接代数与几何的一个纽带，更是数形结合的典范之一.
学生学习 | 基本不等式中的变换技巧

学生学习 | 基本不等式中的变换技巧

摘要：基本不等式及其应用，是高中数学中的一个重要知识点，也是一个基本解题工具.结合基本不等式的应用与关系式的变形与转化，借助合理分拆、巧妙拼装、正确配凑、准确合成等方式加以综合与应用，剖析应用基本不等式的技巧与方式，开拓解题思路，提升数学品质. 关键词：基本不等式；分拆；拼装；配凑；合成基本不等式作为高中数学“不等式”章节的一个重要知识点，一直是历年高考数学试卷中考查的重点与热点.在具体考查
学生学习 | 复数场景创设，几何意义应用

学生学习 | 复数场景创设，几何意义应用

摘要：复数的几何意义是复数自身的延伸与拓展，也是“数”“形”结合的很好例证.结合复数几何意义应用的一些常见场景实例，结合概念、运算、综合问题以及创新问题等方面，剖析复数几何意义应用的内涵实质，归纳总结解题规律与技巧，本文中指导数学教学与复习备考. 关键词：复数；几何意义；概念；运算；综合通过建立平面直角坐标系，引入复平面，就可以把相应的复数（代数问题）转化为复平面内的点（几何问题）来分析与研
学生学习 | 指数函数背景创设，复合函数情境应用

学生学习 | 指数函数背景创设，复合函数情境应用

与指数函数有关的复合函数是指结合指数函数的概念、基本知识与简单函数（一次函数、二次函数等）复合而成的新函数. 解决与指数函数有关的复合函数情境应用问题，通常借助函数的解析式、相关概念、基本性质、函数图象等，结合相关的思维技巧，合理转化，巧妙变换，将复杂的复合函数问题简单化，从而实现问题的分析与解决，提升学生的思维能力. 1 性质问题 1.1 函数的单调性例1 函数f（x）=12x2-2
评价透视 | 直观先行推理为本，选材导学素养是根

评价透视 | 直观先行推理为本，选材导学素养是根

课题信息：四川省教育科研课题“情景教学视域下的高中数学‘教-学-评’一致性研究”，课题编号为YB2023010. 摘要：2023年高考全国甲卷数学试题体现了高考“一核四层四翼”的评价要求，突出考查高中数学六大核心素养，尤其着重考查了直观想象素养，全卷23道题中有15道涉及数学直观，涵盖高中数学的各大主题，分值占比60%以上，这类问题可从直观寻求突破，再用逻辑推理加以论证. 关键词：核心素养；直
评价透视 | 新情境下的解析几何综合题命制

评价透视 | 新情境下的解析几何综合题命制

摘要：通过一道新情境下解析几何试题命制的过程，揭示解析几何试题对于直观想象、数学运算核心素养的培养价值，探索科学备考途径. 关键词：解析几何；试题命制；数学运算 1 原创试题图1是一款新型多功能无人机，兼具航拍、监测、跟踪、定位、巡逻等功能.无人机机架采用对称排列结构便于抵消反扭距，所以旋翼多采用偶数对称排列.其机架形状的俯视图可看作曲线Γ：x4λ2+y4λ2=2x2y2λ2+1（λ>
解题天地 | 多面体体积计算中的多种思维方法

解题天地 | 多面体体积计算中的多种思维方法

空间几何体的体积，依据题设的特殊性可直接用公式、作棱的直截面割补法、三棱锥等体积变换法、分割法、补形法等求解，凸显 “化非规则为规则，化不可求为可求，或化不易求为易求”的整体思维的具体应用.下文主要探究几何体体积计算中的多种思维方法. 1 整体法例1 已知长方体的三个面面积分别为2，3，6，则长方体的体积等于（）. A.6 B.6 C.66 D. 36 解析：设此长方体的长、
解题天地 | 一道高考圆锥曲线题的解法探究与反思

解题天地 | 一道高考圆锥曲线题的解法探究与反思

高考数学真题是众多优秀命题专家精心设计出来的.其中解析几何压轴题，紧扣教材，立足考查学生的能力. 1 试题呈现试题（2020全国I卷理科20题，文科21题）已知A，B分别为椭圆E：x2a2+y2=1（a>1）的左、右顶点，G为E的上顶点，AG·GB=8，P为直线x=6上的动点，PA与E的另一个交点为C，PB与E的另一交点为D. （1）求E的方程; （2）证明：直线CD过定点.
解题天地 | 巧思维切入，妙方法破解

解题天地 | 巧思维切入，妙方法破解

双变元代数式的最值（最大值或最小值）或取值范围问题，是天津高考试卷中一副不变的熟悉“面孔”，创新新颖，常考常新.破解此类问题，结合双变元代数式的基本特征，借助基本不等式思维、函数或方程思维、导数思维或其他重要不等式思维等加以切入与破解，合理融合基本不等式、函数与方程、导数等相关数学知识与数学思想方法，巧妙处理，正确破解. 1 真题呈现高考真题（2021年高考数学天津卷第13题）已知a&g
解题天地 | 四点共面，链接教材，变式拓展

解题天地 | 四点共面，链接教材，变式拓展

空间中的四点共面的判断与证明是空间向量与立体几何部分的一个基本知识点，也是一大难点，历年高考数学试题中较少涉及，没有引起大家的高度重视.而在2020年高考数学全国卷Ⅲ的文科和理科试题中，都出现了空间四点共面的证明问题，也充分说明了该部分知识的基础性与重要性.借助空间中四点共面的判断与证明，很好地考查考生的数形结合思想、空间想象能力与推理论证能力，以及直观想象、逻辑推理等数学核心素养. 1 真题呈
解题天地 | 2023年高考数学全国乙卷第11题的巧思妙变

解题天地 | 2023年高考数学全国乙卷第11题的巧思妙变

摘要：涉及直线与圆的位置关系的综合应用问题，一直是高考中比较常见的基本考点之一.结合一道高考真题，借助圆方程的场景创设，通过不同思维视角来确定一次代数式的最值，多思维层面切入，多技巧视角应用，探究破解问题的思路与变式拓展，指导数学教学与解题研究. 关键词：实数；直线；圆；距离；方程直线与圆是平面解析几何中两类最简单的基本图形，又是初中平面几何中的基本图形之一.直线与圆之间的位置关系问题，有效
解题天地 | 多向思维，多种方法，多类拓展

解题天地 | 多向思维，多种方法，多类拓展

课题信息：福建省石狮市教育科学“十四五”规划（第一批）研究课题“高中数学结构不良型提问预设与生成的优化研究”，课题编号为SGC21-32. 有关多变元代数式（特别是双变元）的最值（或取值范围）问题，是高考、竞赛等数学试卷中比较常见的一类题型.此类问题常以函数或方程的形式出现，巧妙融合函数与方程、不等式等基本知识，常考常新，变化多端，难度中等及偏上，具有较好的选拔性与区分度，同时又有一定的技巧方法
解题天地 | 前沿热点，高考前线——创设情境问题

解题天地 | 前沿热点，高考前线——创设情境问题

随着教育部考试中心关于《中国高考评价体系》（2020年1月）的发布，新高考进一步切实落实高考的“立德树人、服务选才、引导教学”核心功能，为高考各学科命制试题提供了标准与依据，合理指明高考改革的路线与方向.借助指导思想，通过合理创设课程学习情境、探索创新情境和生活实践情境等来实现高考评价，让学生在真实的创新与应用情境中，身临其境，合理抽象，数学建模，进而运用数学基础知识和关键能力来分析、处理与解决相
解题天地 | “解几”背景，“平几”融合：从一道高考试题谈起

解题天地 | “解几”背景，“平几”融合：从一道高考试题谈起

平面解析几何综合问题，经常融入平面几何背景，是基于平面几何知识的进一步提升与拓展，成为高考数学命题中的一个重要场景与应用.在处理此类问题时，经常要合理借助平面几何的直观，把握平面解析几何的实质，进而综合分析与解决问题.同时，此类问题也很好地兼顾了高考数学试题的基础性、综合性、创新型和综合性，以及试题间的层次性，合理调控综合程度. 1 真题呈现高考真题〔2021年高考数学全国甲卷理科第15
解题天地 | 应用齐次化解决解析几何中定点定值问题

解题天地 | 应用齐次化解决解析几何中定点定值问题

摘要：应用齐次化方法解决圆锥曲线定点、定值等问题，成为近年来高考试题的主流趋势.这是一种新型创新方法，倍受高考命题者和高中教师青睐.本文中尝试从斜率基础知识讲起，结合例题力求将齐次化方法讲明白. 关键词：齐次化;平移;构造;二次曲线;定点；定值文＼中，详尽论述了圆锥曲线上不共线三点定理关于定点、定值的问题，提到了利用原点平移法解决复杂的计算.文＼中，阐述了如何突破解析几何中的超量运算问题.两
解题天地 | 二项式定理题型破解思路与策略

解题天地 | 二项式定理题型破解思路与策略

摘要：二项式定理是历年高考考查的热点内容之一，本文中整理了涉及二项式定理的常见题型，如求二项展开式中的特定项或特定项系数问题、与二项展开式中的系数和有关的问题、利用二项式定理处理整除问题以及计算近似值的问题.破解核心在于通过排列组合从本质上理解二项展开式的通项公式，以及掌握赋值法在求解二项展开式系数和问题中的巧妙运用. 关键词：二项式定理；通项公式；赋值法；排列组合二项式定理的起源最早可以追
解题天地 | 一题多解和一题多变：一道有关抛物线焦半径问题的探究

解题天地 | 一题多解和一题多变：一道有关抛物线焦半径问题的探究

课题信息：江苏省教育科学“十四五”规划普教重点课题“指向关键能力的高中数学主题单元式教学的实践研究”，课题编号为B/2021/02/34；江苏省教研室第十一期立项课题“差异教学在课程基地中应用的实践研究”，课题编号为2015JK11-LO42. 抛物线的焦半径问题是抛物线综合问题中的一类特殊类型，其可以联系起抛物线的定义（问题的本质）、几何性质（“数”的属性）与几何特征（“形”的特征）、焦半径公
解题天地 | 直线与圆锥曲线题型及解法探究

解题天地 | 直线与圆锥曲线题型及解法探究

直线与圆锥曲线题型灵活多变，难度较大.为提高学生的解题能力，为其数学水平的提升奠定坚实的基础，教学中应注重相关题型以及解法的汇总、讲解，使学生遇到相关习题时，能够迅速破题，增强解答直线与圆锥曲线问题的自信. 1 直线与圆锥曲线位置问题判断直线与圆锥曲线的位置关系，需要将直线和圆锥曲线方程联立，转化成一元二次方程，借助Δ进行判断.同时，还应注重灵活运用向量知识判断直线与直线的位置关系.另外，如
解题天地 | 立体几何垂直证明思路探究

解题天地 | 立体几何垂直证明思路探究

摘要：立体几何的主要目的是培养学生的空间想象能力，但立体几何的学习对学生而言普遍感到困难.本文中结合具体案例对立体几何垂直关系的证明思路进行了探究，为学生学习立体几何主题提供一些参考. 关键词：立体几何；垂直证明；解题思路立体几何的垂直证明问题可以分为三类，分别是直线与直线、直线与平面、平面与平面.核心分析思路是通过假设待证的结论成立，然后结合已知条件，再进行逆向推理，得到关键信息，从而完成
教师发展 | 晰错因明本质悟方法

教师发展 | 晰错因明本质悟方法

摘要：试卷讲评是高三教学的主流形式，是发展素养的重要土壤.文章以一道高三模考题为例，从错误原因、修正问题、探究本质三个方面进行分析，最后给出优化高三教学的点滴感悟. 关键词：错题；核心素养；优化教学荆岫之玉必含纤瑕，骊龙之珠亦有微纇.一道正确（优美）的题目可以让人赏心悦目，一道错误（瑕疵）的题目同样可以令人遐想万千.本文中笔者以一道错题为例，晰错因、明本质、悟方法. 1 原题呈现例1
教师发展 | 基于核心素养的高中数学教学实践

教师发展 | 基于核心素养的高中数学教学实践

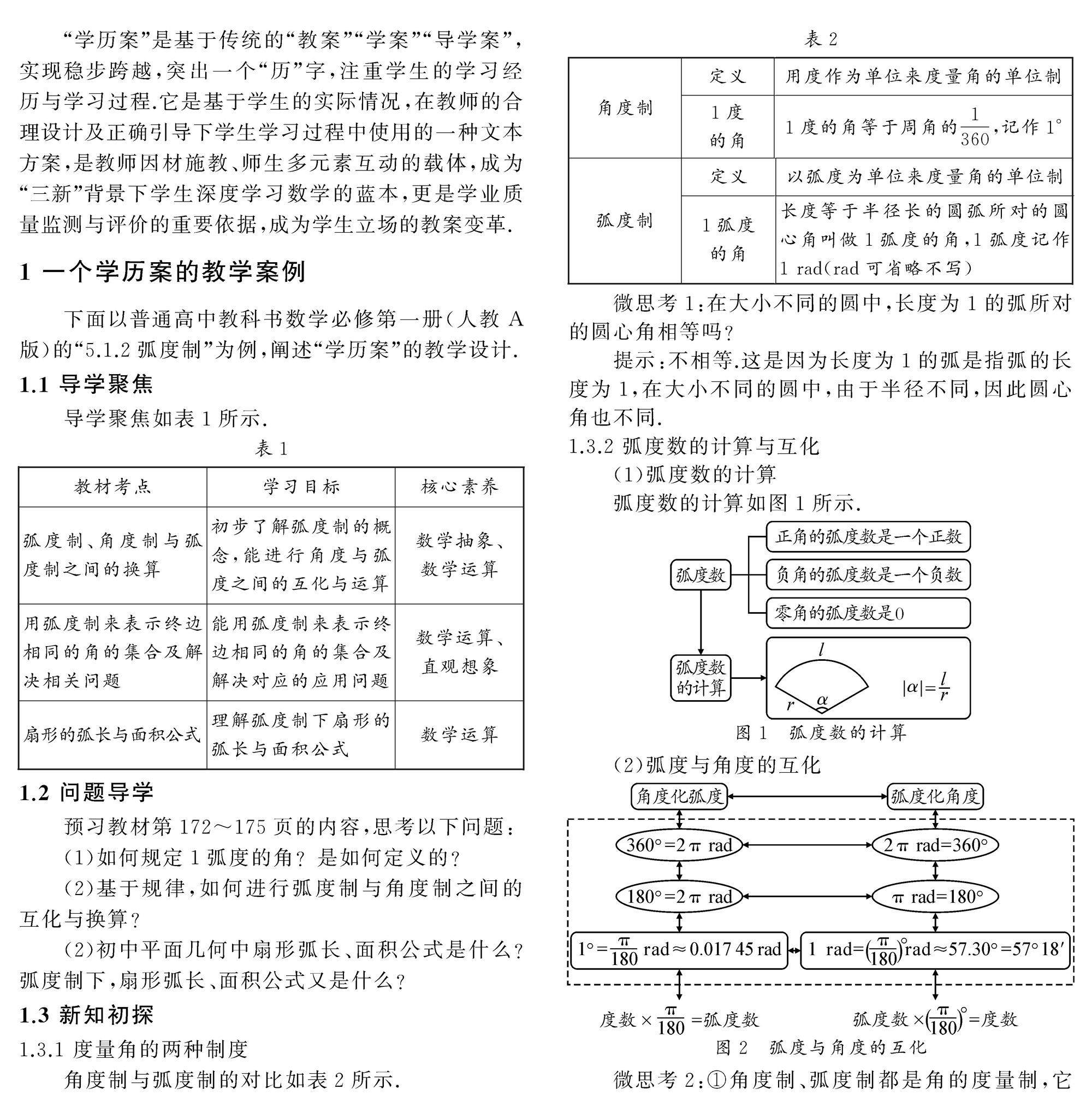
学生核心素养的培养不应局限于知识层面，也应关注能力、态度和价值观的培养，这对促进学生健康成长有着重要的作用.那么，培养学生的核心素养就要改变单一的“灌输式”教学模式，善于借助教学情境来调动学生的主观能动性，注重学生自主学习能力的培养，引导学生积极思考，提升学习的积极性.同时，在教学中要关注个体的发展，引导学生通过合作探究提升综合能力，进而提升教学质量和学生的数学素养.基于此，笔者以培养学生核心素养
教师发展 | 注重学历案的本质，促进学生深度学习

教师发展 | 注重学历案的本质，促进学生深度学习

课题信息：江苏省教育科学“十四五”规划2021年度重点课题“基于学历案的高中数学主题单元教学模式建构与实践探究”，课题编号为B/2021/02/152. “学历案”是基于传统的“教案”“学案”“导学案”，实现稳步跨越，突出一个“历”字，注重学生的学习经历与学习过程.它是基于学生的实际情况，在教师的合理设计及正确引导下学生学习过程中使用的一种文本方案，是教师因材施教、师生多元素互动的载体，成为“三
教师发展 | 三角函数图象与性质促核心素养生成

教师发展 | 三角函数图象与性质促核心素养生成

摘要：三角函数的图象与性质既是高中数学的重要组成部分，也是应用于物理与工程技术领域的知识基础，更是培养学生数学核心素养的重要载体.数学核心素养以“学生本位”的立场，推动学生品格与能力发展.因此，本文中着重探究如何透过学生视角，关注学生在数学小组合作学习中的体验与兴趣以及生活问题与数学问题链接的能力，鼓励学生多维度去理解与应用数学，以提高数学思维能力、问题解决能力、沟通能力. 关键词：数学核心素养

过往期刊

更多

猜你喜欢

泸州市图书馆电子阅览室